The Labour Market and Price and Wage Formation in the Long Run

 

Bengt Assarsson

2004-06-14

 

Introduction

 

The supply side can be described as a price and wage setting model à la Layard-Nickell. In the very simple case such a model has a wage eqution that determines the wage rate at such a high rate that the demand for labour determines the employment rate. A simple production function then determines output while the price level is set as a markup on marginal cost.

 

To give the reader an intuition about the model properties I show the simplest possible specification (which is different from the BASMOD specification) of such a model. The reader is then referred to the specific parts of the labour market in BASMOD which basically works in a similar way.

 

A Simple Basic Specification

 

Let the wage equation be represented by the wage share equation

 

                                                                                                             (1)

 

i.e. the wage share depends on the unemployment rate. W is the nominal wage rate, E is the number of employed persons, P is the general price level, Y is the output level (GDP), U is the unemployment rate and  are parameters. The wage share depends negatively on the unemployment rate and also on the parameter  which is supposed to be a function of structural factors like the replacement ratio, unemployment insurance, etc. Consider then the simple price equation

 

                                                                                                             (2)

 

where  is the markup and  labour productivity. Hence,  approximates marginal cost for the simple production function . (1) and (2) can be rewritten to give

 

                                                                                                         (1’)

 

and

 

                                                                                                                   (2’)

 

In (1’) and (2’) we can solve for the real wage and the rate of unemployment, the latter being

 

                                                                                                            (3)

 

We see that the equilibrium rate of unemployment depends on structural factors (  ), the elasticity of the real wage to the rate of unemployment and the markup which in turn depends on the degree of competition. Note also that the equilibrium unemployment rate is independent of marginal cost. The more competitive markets are the lower the rate of equilibrium unemployment.

 

The rate of unemployment is defined as

 

                                                                                                      (4)

 

where L  is the labour force and hence given the labour force potential output is given by

 

                                                                                          (5)

 

 

Hence, potential output will be determined by the same factors as the equilibrium rate of unemployment and in addition the labour force and the labour productivity. Potential output will grow in line with labour productivity and the labour force and be affected positively by the degree of competitiveness in the markets.

 

(1) to (5) constitutes the basic structure of the supply side or long run equilibrium in the model. This simplified description has been done in order to increase the understanding of the mechanisms in the model. In practice the model is more detailed than this and we now turn to a more detailed description of the structure.

 

The Labour Market in More Detail

 

In the simplified description above we used a production function in which output only depended on labour input. Suppose instead that we use the more general production function

 

                                                                                                            (6)

 

where K is the capital stock and H is the number of hours worked. We also use the  definition

 

                                                                                                                     (7)

 

where  is the mean number of hours worked. HA is the number of efficient hours worked where A is an efficiency index. A can be measured in various ways and BASMOD uses two alternative specifications, one in which A follows a simple time trend and the other more complicated specification in which A depends on the degree of education of  the employed.

 

The specification of (6) and other functions in the model is also a somewhat delicate matter. Macro models often employ simple functional forms – like the Cobb-Douglas. However, empirical studies often tend to reject the simple forms and favour more flexible models like the Translog or different versions of CES. Functional forms and the dynamic specification have been compared in the process of finding a suitable specification.

 

More generally, there is a profit function

 

                                                                  (8)

 

where  is the demand function and  the user cost of capital. An equivalent formulation is

 

                                                                                    (8’)

 

in terms of the shadow wage rate  and efficient hours . With this setup the conventional analysis can be carried out in terms of shadow wages and efficient hours and a suitable specification of the efficiency index. The cost function can be written[1]

 

                                                                                                       (9)

 

The cost function is very important since its partial derivatives determine both the demand for inputs and the marginal cost.

 

The demand for labour is determined by the partial derivative of the cost function w.r.t.  and gives

 

                                                                                                   (10)

 

i.e. hours demanded generally depend on the same variables that enter the cost function. Note also that the demand system – i.e. the demand for labour as well as capital – implies that the demand for capital can be derived as a residual equation once the demand for labour has been estimated and established:

 

                                                                                                        (11)

 

so that the stochastic system implied by (10) – (11) is singular.

 

It is then assumed that the labour market is characterized by union negotiations and that the unions try to achieve a high wage share. We assume that the wage share depends on some structural factors as in (1) and the rate of unemployment. As it turns out, the wage share depends positively on the replacement ratio and negatively on the rate of unemployment [Pissarides, 2000]. It is also assumed that the power of the unions is strong so that the real wage rate ends up at a level above the competitive wage rate. Therefore the demand for labour determines equilibrium in the labour market. The properties of the market is illustrated in the diagram below.

E=H/HM

 

 

 

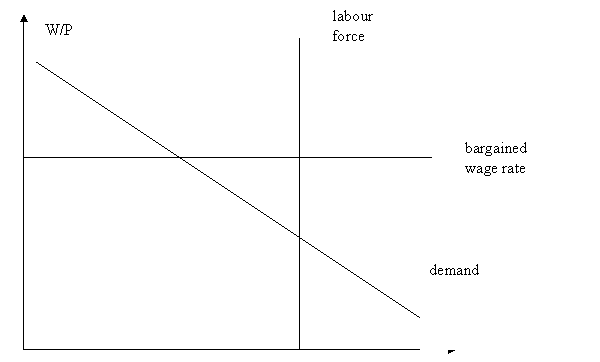
The real wage rate is on the vertical axis and employment on the horizontal axis. The definition (7) is used so that the level of employment is determined once  is determined and the rate of unemployment once the labour force L is determined.

 

The mean number of hours is determined by the equation

 

                                                                                                           (12)

 

and the labour force by the equation

 

                                                                                                               (13)

 

where T is a time trend.

 

This completes the description of the wage-setting mechanism in the supply side of the model.

 

Price Setting

 

To close the model we need a description of price setting. This is naturally added by again using the profit function (8’) and the cost function (9). Assuming firms are monopolists as in (8’) we can derive the first-order condition as

 

where . For the competitive firm with revenues  we obtain . We can also use the general specification

 

                                                                                       (14)

 

where  is an index showing the degree of competition. The price level depends on the degree of competition, the price elasticity of demand, the output level, the wage rate, the efficiency index and the user cost of capital.

 

The rate of unemployment and the level of output is essentially the same in equilibrium as in the simple model.

 

Output can be defined in terms of gross output rather than value added. Then the production function instead could be defined in terms of energy and raw materials prices as well. One would then typically end up with a price equation of the form

 

                                                                          (15)

 

 

Inflation and Price Rigidity

 

It is well-known that prices tend to adjust with a considerable delay, such that it takes time to achieve the long run price levels described above. Therefore, the equation (15) describes the equilibrium price level in the long run, while the short run adjustment requires some special treatment.

 

In the new Keynesian models it is common to use a model for short run pricing emanating from Calvo (1983). In that model there are a number of identical firms where each firm has an exogenous probability for the price to change 1 . This probability is assumed to be independent of the time since the most recent observed price change. The average time during which price is constant then is . The price level is then determined by

 

                                                                                                  (16)                                                                                

where the optimal price depends on the expected future marginal cost. The Phillips curve can be written

 

                                                                                             (17)

 

where E is the expectations operator and . Hence, inflation is a function of unobservable variables. According to Bårdsen et al (2002) (17) can be operationalised as

 

                                                                                                         (18)

 

where  is some approximation to contemporaneous marginal costs. Bårdsen et al show that the econometric difficulties embodied in the model are huge and it seems that there does not exist any universally acceptable solution to the problems.

 

Some alternatives are available, one of which is take account of the distribution of relative price changes, as suggested by Ball and Mankiw (1995). Their theory suggests that one should include higher moments of relative price changes – variance and skewness – in the specification of Phillips curves. These variables reflects the effects of short run price rigidity on price formation and hence complements the long run equilibrium relation in (15).